参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
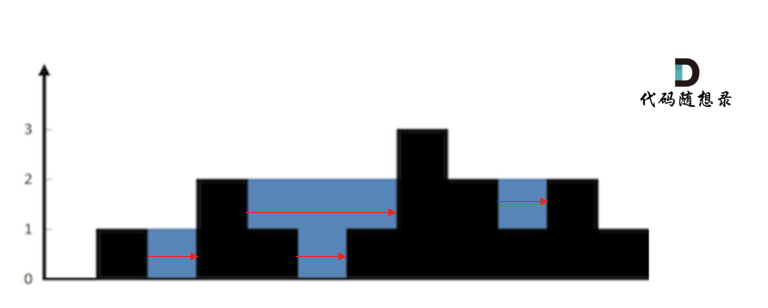
这个图就是大厂面试经典题目,接雨水! 最常青藤的一道题,面试官百出不厌!
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
- 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
- 输出:6
- 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
- 输入:height = [4,2,0,3,2,5]
- 输出:9
《代码随想录》算法视频公开课:单调栈,经典来袭!LeetCode:42.接雨水,相信结合视频在看本篇题解,更有助于大家对本题的理解。
接雨水问题在面试中还是常见题目的,有必要好好讲一讲。
本文深度讲解如下三种方法:
- 暴力解法
- 双指针优化
- 单调栈
本题暴力解法也是也是使用双指针。
首先要明确,要按照行来计算,还是按照列来计算。
一些同学在实现的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
我个人倾向于按照列来计算,比较容易理解,接下来看一下按照列如何计算。
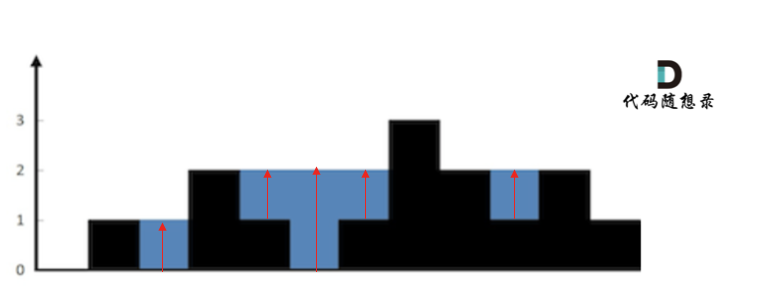
首先,如果按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。
可以看出每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
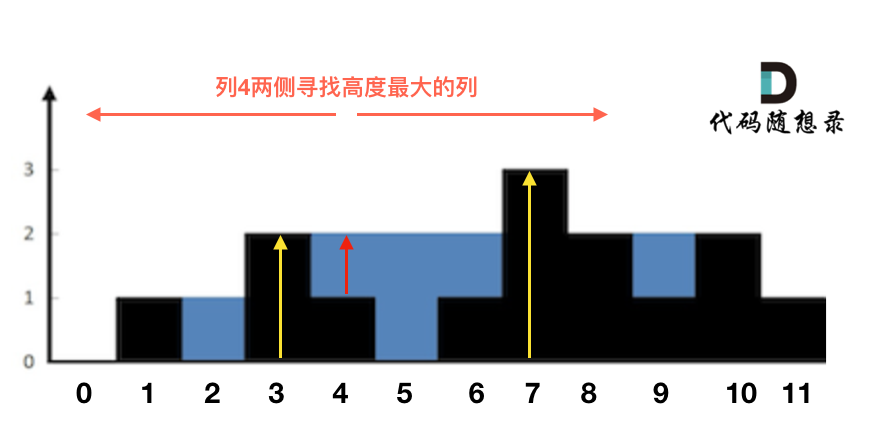
这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
列4 柱子的高度为1(以下用height表示)
那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
此时求出了列4的雨水体积。
一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
首先从头遍历所有的列,并且要注意第一个柱子和最后一个柱子不接雨水,代码如下:
for (int i = 0; i < height.size(); i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i == 0 || i == height.size() - 1) continue;
}在for循环中求左右两边最高柱子,代码如下:
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}最后,计算该列的雨水高度,代码如下:
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h; // 注意只有h大于零的时候,在统计到总和中整体代码如下:
class Solution {
public:
int trap(vector<int>& height) {
int sum = 0;
for (int i = 0; i < height.size(); i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i == 0 || i == height.size() - 1) continue;
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h;
}
return sum;
}
};因为每次遍历列的时候,还要向两边寻找最高的列,所以时间复杂度为O(n^2),空间复杂度为O(1)。
力扣后面修改了后台测试数据,所以以上暴力解法超时了。
在暴力解法中,我们可以看到只要记录左边柱子的最高高度 和 右边柱子的最高高度,就可以计算当前位置的雨水面积,这就是通过列来计算。
当前列雨水面积:min(左边柱子的最高高度,记录右边柱子的最高高度) - 当前柱子高度。
为了得到两边的最高高度,使用了双指针来遍历,每到一个柱子都向两边遍历一遍,这其实是有重复计算的。我们把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight),这样就避免了重复计算。
当前位置,左边的最高高度是前一个位置的左边最高高度和本高度的最大值。
即从左向右遍历:maxLeft[i] = max(height[i], maxLeft[i - 1]);
从右向左遍历:maxRight[i] = max(height[i], maxRight[i + 1]);
代码如下:
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() <= 2) return 0;
vector<int> maxLeft(height.size(), 0);
vector<int> maxRight(height.size(), 0);
int size = maxRight.size();
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for (int i = 1; i < size; i++) {
maxLeft[i] = max(height[i], maxLeft[i - 1]);
}
// 记录每个柱子右边柱子最大高度
maxRight[size - 1] = height[size - 1];
for (int i = size - 2; i >= 0; i--) {
maxRight[i] = max(height[i], maxRight[i + 1]);
}
// 求和
int sum = 0;
for (int i = 0; i < size; i++) {
int count = min(maxLeft[i], maxRight[i]) - height[i];
if (count > 0) sum += count;
}
return sum;
}
};关于单调栈的理论基础,单调栈适合解决什么问题,单调栈的工作过程,大家可以先看这题讲解 739. 每日温度。
单调栈就是保持栈内元素有序。和栈与队列:单调队列一样,需要我们自己维持顺序,没有现成的容器可以用。
通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。
而接雨水这道题目,我们正需要寻找一个元素,右边最大元素以及左边最大元素,来计算雨水面积。
那么本题使用单调栈有如下几个问题:
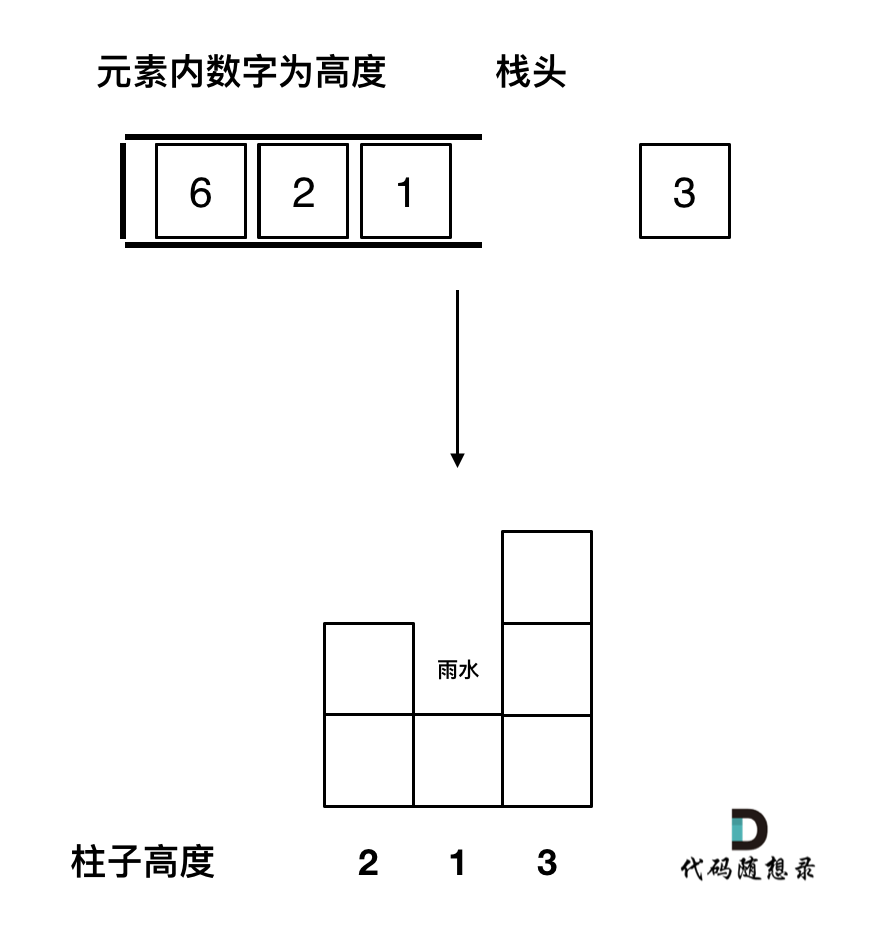
- 首先单调栈是按照行方向来计算雨水,如图:
知道这一点,后面的就可以理解了。
- 使用单调栈内元素的顺序
从大到小还是从小到大呢?
从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。
因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
如图:
关于单调栈的顺序给大家一个总结: 739. 每日温度 中求一个元素右边第一个更大元素,单调栈就是递增的,84.柱状图中最大的矩形求一个元素右边第一个更小元素,单调栈就是递减的。
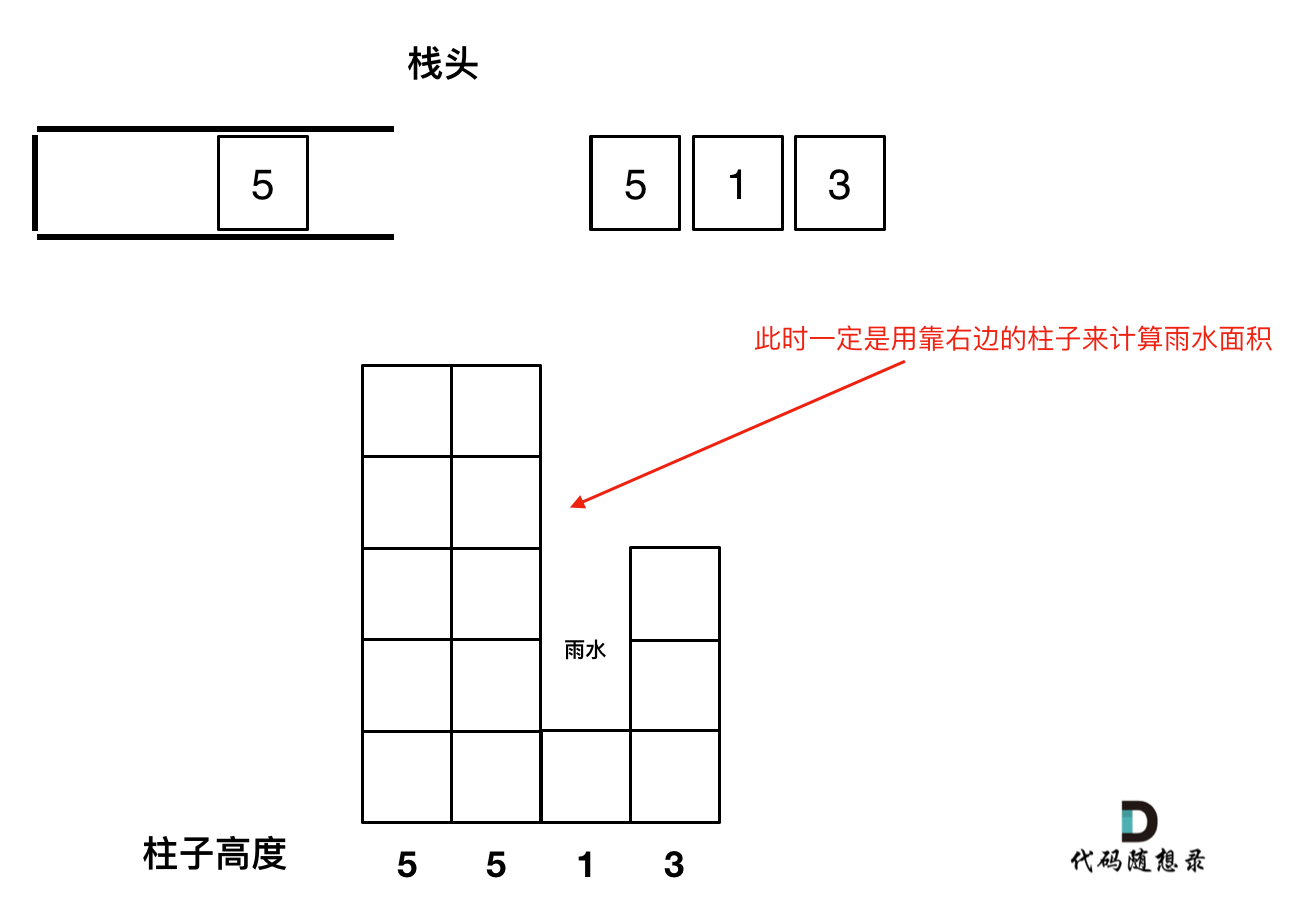
- 遇到相同高度的柱子怎么办。
遇到相同的元素,更新栈内下标,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出,把第二个5添加到栈中。
因为我们要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度。
如图所示:
- 栈里要保存什么数值
使用单调栈,也是通过 长 * 宽 来计算雨水面积的。
长就是通过柱子的高度来计算,宽是通过柱子之间的下标来计算,
那么栈里有没有必要存一个pair<int, int>类型的元素,保存柱子的高度和下标呢。
其实不用,栈里就存放下标就行,想要知道对应的高度,通过height[stack.top()] 就知道弹出的下标对应的高度了。
所以栈的定义如下:
stack<int> st; // 存着下标,计算的时候用下标对应的柱子高度
明确了如上几点,我们再来看处理逻辑。
以下操作过程其实和 739. 每日温度 也是一样的,建议先做 739. 每日温度。
以下逻辑主要就是三种情况
- 情况一:当前遍历的元素(柱子)高度小于栈顶元素的高度 height[i] < height[st.top()]
- 情况二:当前遍历的元素(柱子)高度等于栈顶元素的高度 height[i] == height[st.top()]
- 情况三:当前遍历的元素(柱子)高度大于栈顶元素的高度 height[i] > height[st.top()]
先将下标0的柱子加入到栈中,st.push(0);。 栈中存放我们遍历过的元素,所以先将下标0加进来。
然后开始从下标1开始遍历所有的柱子,for (int i = 1; i < height.size(); i++)。
如果当前遍历的元素(柱子)高度小于栈顶元素的高度,就把这个元素加入栈中,因为栈里本来就要保持从小到大的顺序(从栈头到栈底)。
代码如下:
if (height[i] < height[st.top()]) st.push(i);
如果当前遍历的元素(柱子)高度等于栈顶元素的高度,要跟更新栈顶元素,因为遇到相相同高度的柱子,需要使用最右边的柱子来计算宽度。
代码如下:
if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况
st.pop();
st.push(i);
}
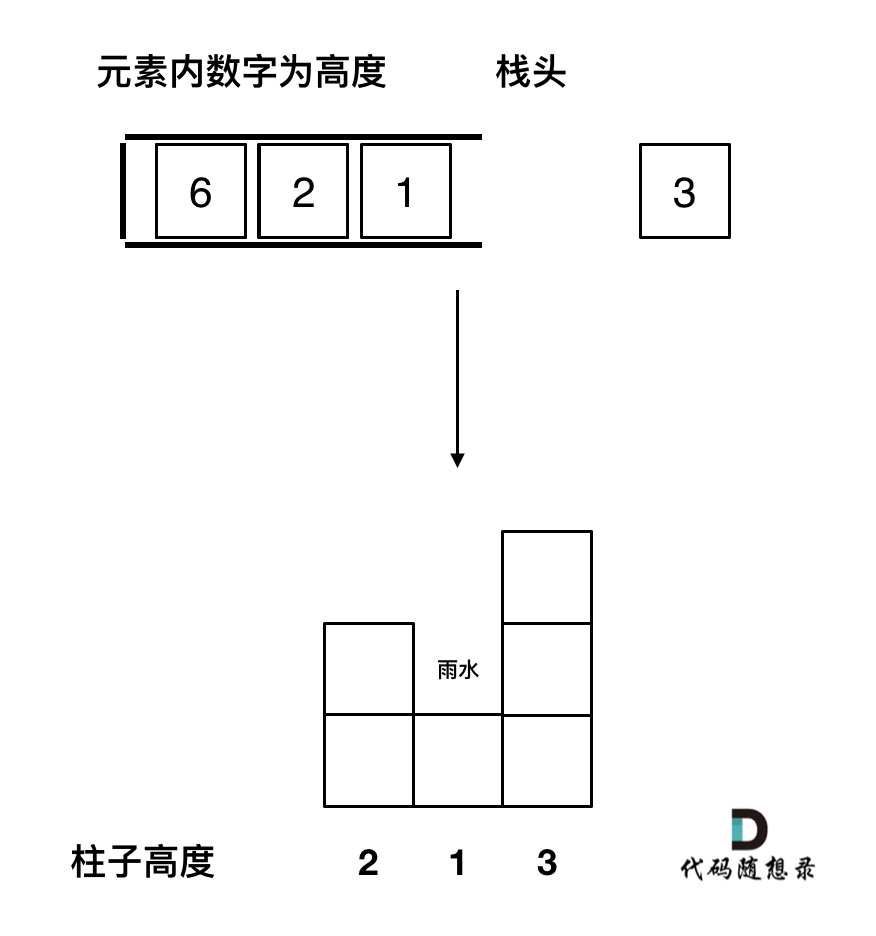
如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid](就是图中的高度1)。
此时的栈顶元素st.top(),就是凹槽的左边位置,下标为st.top(),对应的高度为height[st.top()](就是图中的高度2)。
当前遍历的元素i,就是凹槽右边的位置,下标为i,对应的高度为height[i](就是图中的高度3)。
此时大家应该可以发现其实就是栈顶和栈顶的下一个元素以及要入栈的元素,三个元素来接水!
那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:int h = min(height[st.top()], height[i]) - height[mid];
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度),代码为:int w = i - st.top() - 1 ;
当前凹槽雨水的体积就是:h * w。
求当前凹槽雨水的体积代码如下:
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while,持续跟新栈顶元素
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1; // 注意减一,只求中间宽度
sum += h * w;
}
}关键部分讲完了,整体代码如下:
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() <= 2) return 0; // 可以不加
stack<int> st; // 存着下标,计算的时候用下标对应的柱子高度
st.push(0);
int sum = 0;
for (int i = 1; i < height.size(); i++) {
if (height[i] < height[st.top()]) { // 情况一
st.push(i);
} if (height[i] == height[st.top()]) { // 情况二
st.pop(); // 其实这一句可以不加,效果是一样的,但处理相同的情况的思路却变了。
st.push(i);
} else { // 情况三
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1; // 注意减一,只求中间宽度
sum += h * w;
}
}
st.push(i);
}
}
return sum;
}
};以上代码冗余了一些,但是思路是清晰的,下面我将代码精简一下,如下:
class Solution {
public:
int trap(vector<int>& height) {
stack<int> st;
st.push(0);
int sum = 0;
for (int i = 1; i < height.size(); i++) {
while (!st.empty() && height[i] > height[st.top()]) {
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1;
sum += h * w;
}
}
st.push(i);
}
return sum;
}
};精简之后的代码,大家就看不出去三种情况的处理了,貌似好像只处理的情况三,其实是把情况一和情况二融合了。 这样的代码不太利于理解。
暴力解法:
class Solution {
public int trap(int[] height) {
int sum = 0;
for (int i = 0; i < height.length; i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i==0 || i== height.length - 1) continue;
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i+1; r < height.length; r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i-1; l >= 0; l--) {
if(height[l] > lHeight) lHeight = height[l];
}
int h = Math.min(lHeight, rHeight) - height[i];
if (h > 0) sum += h;
}
return sum;
}
}双指针:
class Solution {
public int trap(int[] height) {
int length = height.length;
if (length <= 2) return 0;
int[] maxLeft = new int[length];
int[] maxRight = new int[length];
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for (int i = 1; i< length; i++) maxLeft[i] = Math.max(height[i], maxLeft[i-1]);
// 记录每个柱子右边柱子最大高度
maxRight[length - 1] = height[length - 1];
for(int i = length - 2; i >= 0; i--) maxRight[i] = Math.max(height[i], maxRight[i+1]);
// 求和
int sum = 0;
for (int i = 0; i < length; i++) {
int count = Math.min(maxLeft[i], maxRight[i]) - height[i];
if (count > 0) sum += count;
}
return sum;
}
}双指针优化
class Solution {
public int trap(int[] height) {
if (height.length <= 2) {
return 0;
}
// 从两边向中间寻找最值
int maxLeft = height[0], maxRight = height[height.length - 1];
int l = 1, r = height.length - 2;
int res = 0;
while (l <= r) {
// 不确定上一轮是左边移动还是右边移动,所以两边都需更新最值
maxLeft = Math.max(maxLeft, height[l]);
maxRight = Math.max(maxRight, height[r]);
// 最值较小的一边所能装的水量已定,所以移动较小的一边。
if (maxLeft < maxRight) {
res += maxLeft - height[l ++];
} else {
res += maxRight - height[r --];
}
}
return res;
}
}单调栈法
class Solution {
public int trap(int[] height){
int size = height.length;
if (size <= 2) return 0;
// in the stack, we push the index of array
// using height[] to access the real height
Stack<Integer> stack = new Stack<Integer>();
stack.push(0);
int sum = 0;
for (int index = 1; index < size; index++){
int stackTop = stack.peek();
if (height[index] < height[stackTop]){
stack.push(index);
}else if (height[index] == height[stackTop]){
// 因为相等的相邻墙,左边一个是不可能存放雨水的,所以pop左边的index, push当前的index
stack.pop();
stack.push(index);
}else{
//pop up all lower value
int heightAtIdx = height[index];
while (!stack.isEmpty() && (heightAtIdx > height[stackTop])){
int mid = stack.pop();
if (!stack.isEmpty()){
int left = stack.peek();
int h = Math.min(height[left], height[index]) - height[mid];
int w = index - left - 1;
int hold = h * w;
if (hold > 0) sum += hold;
stackTop = stack.peek();
}
}
stack.push(index);
}
}
return sum;
}
}暴力解法:
class Solution:
def trap(self, height: List[int]) -> int:
res = 0
for i in range(len(height)):
if i == 0 or i == len(height)-1: continue
lHight = height[i-1]
rHight = height[i+1]
for j in range(i-1):
if height[j] > lHight:
lHight = height[j]
for k in range(i+2,len(height)):
if height[k] > rHight:
rHight = height[k]
res1 = min(lHight,rHight) - height[i]
if res1 > 0:
res += res1
return res双指针:
class Solution:
def trap(self, height: List[int]) -> int:
leftheight, rightheight = [0]*len(height), [0]*len(height)
leftheight[0]=height[0]
for i in range(1,len(height)):
leftheight[i]=max(leftheight[i-1],height[i])
rightheight[-1]=height[-1]
for i in range(len(height)-2,-1,-1):
rightheight[i]=max(rightheight[i+1],height[i])
result = 0
for i in range(0,len(height)):
summ = min(leftheight[i],rightheight[i])-height[i]
result += summ
return result单调栈
class Solution:
def trap(self, height: List[int]) -> int:
# 单调栈
'''
单调栈是按照 行 的方向来计算雨水
从栈顶到栈底的顺序:从小到大
通过三个元素来接水:栈顶,栈顶的下一个元素,以及即将入栈的元素
雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度)
'''
# stack储存index,用于计算对应的柱子高度
stack = [0]
result = 0
for i in range(1, len(height)):
# 情况一
if height[i] < height[stack[-1]]:
stack.append(i)
# 情况二
# 当当前柱子高度和栈顶一致时,左边的一个是不可能存放雨水的,所以保留右侧新柱子
# 需要使用最右边的柱子来计算宽度
elif height[i] == height[stack[-1]]:
stack.pop()
stack.append(i)
# 情况三
else:
# 抛出所有较低的柱子
while stack and height[i] > height[stack[-1]]:
# 栈顶就是中间的柱子:储水槽,就是凹槽的地步
mid_height = height[stack[-1]]
stack.pop()
if stack:
right_height = height[i]
left_height = height[stack[-1]]
# 两侧的较矮一方的高度 - 凹槽底部高度
h = min(right_height, left_height) - mid_height
# 凹槽右侧下标 - 凹槽左侧下标 - 1: 只求中间宽度
w = i - stack[-1] - 1
# 体积:高乘宽
result += h * w
stack.append(i)
return result
# 单调栈压缩版
class Solution:
def trap(self, height: List[int]) -> int:
stack = [0]
result = 0
for i in range(1, len(height)):
while stack and height[i] > height[stack[-1]]:
mid_height = stack.pop()
if stack:
# 雨水高度是 min(凹槽左侧高度, 凹槽右侧高度) - 凹槽底部高度
h = min(height[stack[-1]], height[i]) - height[mid_height]
# 雨水宽度是 凹槽右侧的下标 - 凹槽左侧的下标 - 1
w = i - stack[-1] - 1
# 累计总雨水体积
result += h * w
stack.append(i)
return resultfunc trap(height []int) int {
var left, right, leftMax, rightMax, res int
right = len(height) - 1
for left < right {
if height[left] < height[right] {
if height[left] >= leftMax {
leftMax = height[left] // 设置左边最高柱子
} else {
res += leftMax - height[left] // //右边必定有柱子挡水,所以遇到所有值小于等于leftMax的,全部加入水池中
}
left++
} else {
if height[right] > rightMax {
rightMax = height[right] // //设置右边最高柱子
} else {
res += rightMax - height[right] // //左边必定有柱子挡水,所以,遇到所有值小于等于rightMax的,全部加入水池
}
right--
}
}
return res
}双指针解法:
func trap(height []int) int {
sum:=0
n:=len(height)
lh:=make([]int,n)
rh:=make([]int,n)
lh[0]=height[0]
rh[n-1]=height[n-1]
for i:=1;i<n;i++{
lh[i]=max(lh[i-1],height[i])
}
for i:=n-2;i>=0;i--{
rh[i]=max(rh[i+1],height[i])
}
for i:=1;i<n-1;i++{
h:=min(rh[i],lh[i])-height[i]
if h>0{
sum+=h
}
}
return sum
}
func max(a,b int)int{
if a>b{
return a
}
return b
}
func min(a,b int)int{
if a<b{
return a
}
return b
}单调栈解法
func trap(height []int) int {
if len(height) <= 2 {
return 0
}
st := make([]int, 1, len(height)) // 切片模拟单调栈,st存储的是高度数组下标
var res int
for i := 1; i < len(height); i++ {
if height[i] < height[st[len(st)-1]] {
st = append(st, i)
} else if height[i] == height[st[len(st)-1]] {
st = st[:len(st)-1] // 比较的新元素和栈顶的元素相等,去掉栈中的,入栈新元素下标
st = append(st, i)
} else {
for len(st) != 0 && height[i] > height[st[len(st)-1]] {
top := st[len(st)-1]
st = st[:len(st)-1]
if len(st) != 0 {
tmp := (min(height[i], height[st[len(st)-1]]) - height[top]) * (i - st[len(st)-1] - 1)
res += tmp
}
}
st = append(st, i)
}
}
return res
}
func min(x, y int) int {
if x >= y {
return y
}
return x
}单调栈压缩版:
func trap(height []int) int {
stack := make([]int, 0)
res := 0
// 无需事先将第一个柱子的坐标入栈,因为它会在该for循环的最后入栈
for i := 0; i < len(height); i ++ {
// 满足栈不为空并且当前柱子高度大于栈顶对应的柱子高度的情况时
for len(stack) > 0 && height[stack[len(stack) - 1]] < height[i] {
// 获得凹槽高度
mid := height[stack[len(stack) - 1]]
// 凹槽坐标出栈
stack = stack[: len(stack) - 1]
// 如果栈不为空则此时栈顶元素为左侧柱子坐标
if len(stack) > 0 {
// 求得雨水高度
h := min(height[i], height[stack[len(stack) - 1]]) - mid
// 求得雨水宽度
w := i - stack[len(stack) - 1] - 1
res += h * w
}
}
// 如果栈为空或者当前柱子高度小于等于栈顶对应的柱子高度时入栈
stack = append(stack, i)
}
return res
}
func min(x, y int) int {
if x < y {
return x
}
return y
}//暴力解法
var trap = function(height) {
const len = height.length;
let sum = 0;
for(let i = 0; i < len; i++){
// 第一个柱子和最后一个柱子不接雨水
if(i == 0 || i == len - 1) continue;
let rHeight = height[i]; // 记录右边柱子的最高高度
let lHeight = height[i]; // 记录左边柱子的最高高度
for(let r = i + 1; r < len; r++){
if(height[r] > rHeight) rHeight = height[r];
}
for(let l = i - 1; l >= 0; l--){
if(height[l] > lHeight) lHeight = height[l];
}
let h = Math.min(lHeight, rHeight) - height[i];
if(h > 0) sum += h;
}
return sum;
};
//双指针
var trap = function(height) {
const len = height.length;
if(len <= 2) return 0;
const maxLeft = new Array(len).fill(0);
const maxRight = new Array(len).fill(0);
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for(let i = 1; i < len; i++){
maxLeft[i] = Math.max(height[i], maxLeft[i - 1]);
}
// 记录每个柱子右边柱子最大高度
maxRight[len - 1] = height[len - 1];
for(let i = len - 2; i >= 0; i--){
maxRight[i] = Math.max(height[i], maxRight[i + 1]);
}
// 求和
let sum = 0;
for(let i = 0; i < len; i++){
let count = Math.min(maxLeft[i], maxRight[i]) - height[i];
if(count > 0) sum += count;
}
return sum;
};
//单调栈 js数组作为栈
var trap = function(height) {
const len = height.length;
if(len <= 2) return 0; // 可以不加
const st = [];// 存着下标,计算的时候用下标对应的柱子高度
st.push(0);
let sum = 0;
for(let i = 1; i < len; i++){
if(height[i] < height[st[st.length - 1]]){ // 情况一
st.push(i);
}
if (height[i] == height[st[st.length - 1]]) { // 情况二
st.pop(); // 其实这一句可以不加,效果是一样的,但处理相同的情况的思路却变了。
st.push(i);
} else { // 情况三
while (st.length !== 0 && height[i] > height[st[st.length - 1]]) { // 注意这里是while
let mid = st[st.length - 1];
st.pop();
if (st.length !== 0) {
let h = Math.min(height[st[st.length - 1]], height[i]) - height[mid];
let w = i - st[st.length - 1] - 1; // 注意减一,只求中间宽度
sum += h * w;
}
}
st.push(i);
}
}
return sum;
};
//单调栈 简洁版本 只处理情况三
var trap = function(height) {
const len = height.length;
if(len <= 2) return 0; // 可以不加
const st = [];// 存着下标,计算的时候用下标对应的柱子高度
st.push(0);
let sum = 0;
for(let i = 1; i < len; i++){ // 只处理的情况三,其实是把情况一和情况二融合了
while (st.length !== 0 && height[i] > height[st[st.length - 1]]) { // 注意这里是while
let mid = st[st.length - 1];
st.pop();
if (st.length !== 0) {
let h = Math.min(height[st[st.length - 1]], height[i]) - height[mid];
let w = i - st[st.length - 1] - 1; // 注意减一,只求中间宽度
sum += h * w;
}
}
st.push(i);
}
return sum;
};暴力解法:
function trap(height: number[]): number {
const length: number = height.length;
let resVal: number = 0;
for (let i = 0; i < length; i++) {
let leftMaxHeight: number = height[i],
rightMaxHeight: number = height[i];
let leftIndex: number = i - 1,
rightIndex: number = i + 1;
while (leftIndex >= 0) {
if (height[leftIndex] > leftMaxHeight)
leftMaxHeight = height[leftIndex];
leftIndex--;
}
while (rightIndex < length) {
if (height[rightIndex] > rightMaxHeight)
rightMaxHeight = height[rightIndex];
rightIndex++;
}
resVal += Math.min(leftMaxHeight, rightMaxHeight) - height[i];
}
return resVal;
};双指针:
function trap(height: number[]): number {
const length: number = height.length;
const leftMaxHeightDp: number[] = [],
rightMaxHeightDp: number[] = [];
leftMaxHeightDp[0] = height[0];
rightMaxHeightDp[length - 1] = height[length - 1];
for (let i = 1; i < length; i++) {
leftMaxHeightDp[i] = Math.max(height[i], leftMaxHeightDp[i - 1]);
}
for (let i = length - 2; i >= 0; i--) {
rightMaxHeightDp[i] = Math.max(height[i], rightMaxHeightDp[i + 1]);
}
let resVal: number = 0;
for (let i = 0; i < length; i++) {
resVal += Math.min(leftMaxHeightDp[i], rightMaxHeightDp[i]) - height[i];
}
return resVal;
};单调栈:
function trap(height: number[]): number {
const length: number = height.length;
const stack: number[] = [];
stack.push(0);
let resVal: number = 0;
for (let i = 1; i < length; i++) {
let top = stack[stack.length - 1];
if (height[top] > height[i]) {
stack.push(i);
} else if (height[top] === height[i]) {
stack.pop();
stack.push(i);
} else {
while (stack.length > 0 && height[top] < height[i]) {
let mid = stack.pop();
if (stack.length > 0) {
let left = stack[stack.length - 1];
let h = Math.min(height[left], height[i]) - height[mid];
let w = i - left - 1;
resVal += h * w;
top = stack[stack.length - 1];
}
}
stack.push(i);
}
}
return resVal;
};一种更简便的双指针方法:
之前的双指针方法的原理是固定“底”的位置,往两边找比它高的“壁”,循环若干次求和。
我们逆向思维,把“壁”用两个初始位置在数组首末位置的指针表示,“壁”往中间推,同样可以让每个“底”都能找到最高的“壁”
本质上就是改变了运算方向,从而减少了重复运算
代码如下:
int trap(int* height, int heightSize) {
int ans = 0;
int left = 0, right = heightSize - 1; //初始化两个指针到左右两边
int leftMax = 0, rightMax = 0; //这两个值用来记录左右的“壁”的最高值
while (left < right) { //两个指针重合就结束
leftMax = fmax(leftMax, height[left]);
rightMax = fmax(rightMax, height[right]);
if (leftMax < rightMax) {
ans += leftMax - height[left]; //这里考虑的是下标为left的“底”能装多少水
++left;//指针的移动次序是这个方法的关键
//这里左指针右移是因为左“墙”较矮,左边这一片实际情况下的盛水量是受制于这个矮的左“墙”的
//而较高的右边在实际情况下的限制条件可能不是当前的左“墙”,比如限制条件可能是右“墙”,就能装更高的水,
}
else {
ans += rightMax - height[right]; //同理,考虑下标为right的元素
--right;
}
}
return ans;
}- 时间复杂度 O(n)
- 空间复杂度 O(1)
双指针
impl Solution {
pub fn trap(height: Vec<i32>) -> i32 {
let n = height.len();
let mut max_left = vec![0; height.len()];
let mut max_right = vec![0; height.len()];
max_left.iter_mut().zip(max_right.iter_mut().rev()).enumerate().fold((0, 0), |(lm, rm), (idx, (x, y))| {
let lmax = lm.max(height[idx]);
let rmax = rm.max(height[n - 1 - idx]);
*x = lmax; *y = rmax;
(lmax, rmax)
});
height.iter().enumerate().fold(0, |acc, (idx, x)| {
let h = max_left[idx].min(max_right[idx]);
if h > 0 { h - x + acc } else { acc }
})
}
}单调栈
impl Solution {
pub fn trap(height: Vec<i32>) -> i32 {
let mut stack = vec![];
let mut ans = 0;
for (right_pos, &right_h) in height.iter().enumerate() {
while !stack.is_empty() && height[*stack.last().unwrap()] <= right_h {
let mid_pos = stack.pop().unwrap();
if !stack.is_empty() {
let left_pos = *stack.last().unwrap();
let left_h = height[left_pos];
let top = std::cmp::min(left_h, right_h);
if top > height[mid_pos] {
ans += (top - height[mid_pos]) * (right_pos - left_pos - 1) as i32;
}
}
}
stack.push(right_pos);
}
ans
}
}Rust
双指针
impl Solution {
pub fn trap(height: Vec<i32>) -> i32 {
let n = height.len();
let mut max_left = vec![0; height.len()];
let mut max_right = vec![0; height.len()];
max_left.iter_mut().zip(max_right.iter_mut().rev()).enumerate().fold((0, 0), |(lm, rm), (idx, (x, y))| {
let lmax = lm.max(height[idx]);
let rmax = rm.max(height[n - 1 - idx]);
*x = lmax; *y = rmax;
(lmax, rmax)
});
height.iter().enumerate().fold(0, |acc, (idx, x)| {
let h = max_left[idx].min(max_right[idx]);
if h > 0 { h - x + acc } else { acc }
})
}
}单调栈
impl Solution {
pub fn trap(height: Vec<i32>) -> i32 {
let mut stack = vec![];
let mut ans = 0;
for (right_pos, &right_h) in height.iter().enumerate() {
while !stack.is_empty() && height[*stack.last().unwrap()] <= right_h {
let mid_pos = stack.pop().unwrap();
if !stack.is_empty() {
let left_pos = *stack.last().unwrap();
let left_h = height[left_pos];
let top = std::cmp::min(left_h, right_h);
if top > height[mid_pos] {
ans += (top - height[mid_pos]) * (right_pos - left_pos - 1) as i32;
}
}
}
stack.push(right_pos);
}
ans
}
}