参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！

684.冗余连接

树可以看成是一个连通且无环的无向图。

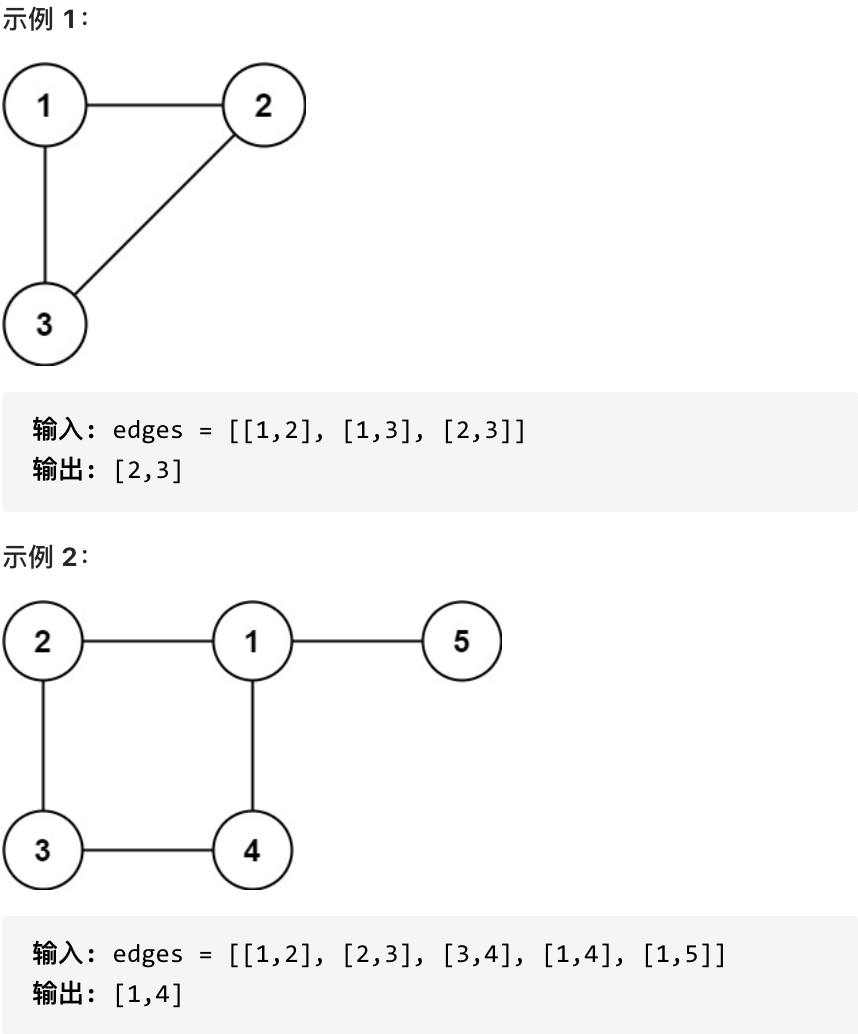
给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

提示:

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

思路

这道题目也是并查集基础题目。

首先要知道并查集可以解决什么问题呢？

主要就是集合问题，两个节点在不在一个集合，也可以将两个节点添加到一个集合中。

这里整理出我的并查集模板如下：

int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构

// 并查集初始化
void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}
// 并查集里寻根的过程
int find(int u) {
    return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}

// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

// 将v->u 这条边加入并查集
void join(int u, int v) {
    u = find(u); // 寻找u的根
    v = find(v); // 寻找v的根
    if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
    father[v] = u;
}

以上模板只要修改 n 就可以了，本题节点数量不会超过1000。

并查集主要有三个功能。

寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点

如果还不了解并查集，可以看这里：并查集理论基础

我们再来看一下这道题目。

题目说是无向图，返回一条可以删去的边，使得结果图是一个有着N个节点的树（即：只有一个根节点）。

如果有多个答案，则返回二维数组中最后出现的边。

那么我们就可以从前向后遍历每一条边（因为优先让前面的边连上），边的两个节点如果不在同一个集合，就加入集合（即：同一个根节点）。

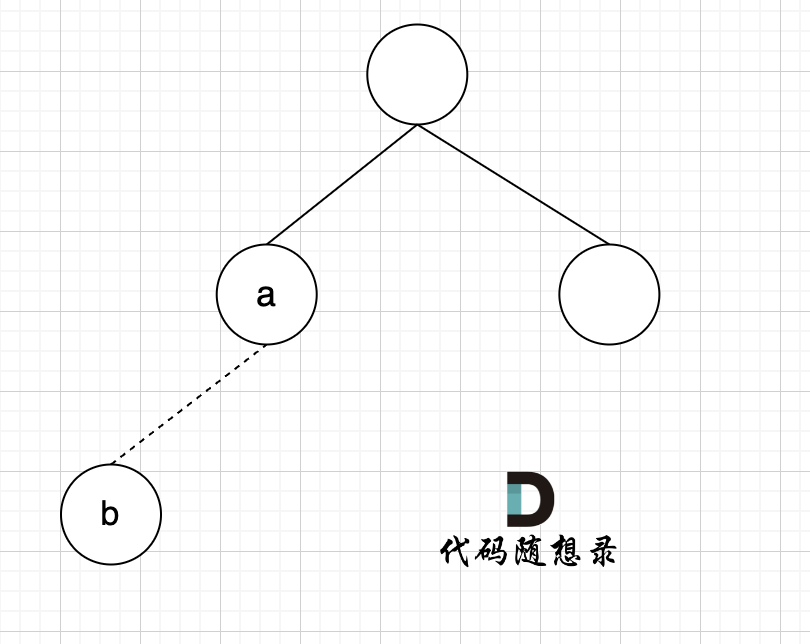
如图所示：

节点A 和节点 B 不在同一个集合，那么就可以将两个节点连在一起。

（如果题目中说：如果有多个答案，则返回二维数组中最前出现的边。那我们就要从后向前遍历每一条边了）

如果边的两个节点已经出现在同一个集合里，说明着边的两个节点已经连在一起了，再加入这条边一定就出现环了。

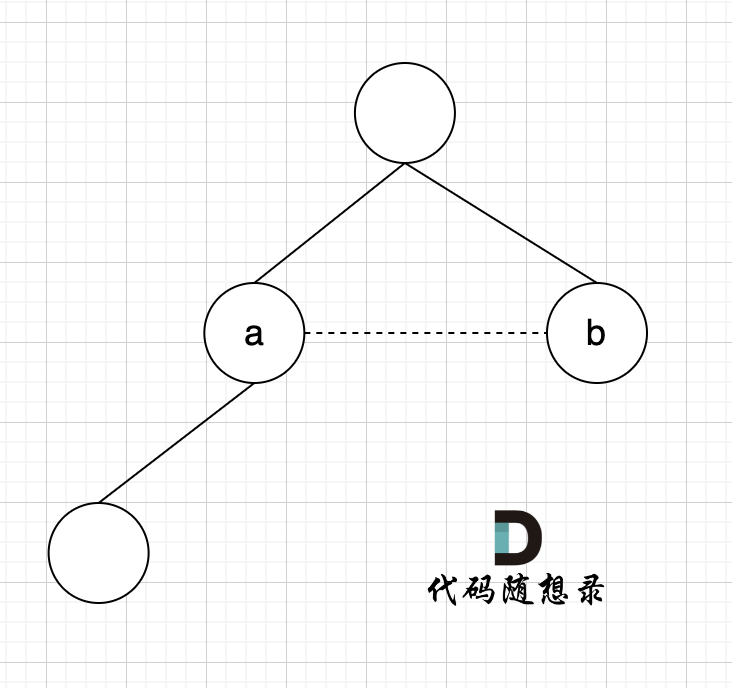
如图所示：

已经判断节点A 和节点B 在在同一个集合（同一个根），如果将节点A 和节点B 连在一起就一定会出现环。

这个思路清晰之后，代码就很好写了。

并查集C++代码如下：

class Solution {
private:
    int n = 1005; // 节点数量3 到 1000
    vector<int> father = vector<int> (n, 0); // C++里的一种数组结构

    // 并查集初始化
    void init() {
        for (int i = 0; i < n; ++i) {
            father[i] = i;
        }
    }
    // 并查集里寻根的过程
    int find(int u) {
        return u == father[u] ? u : father[u] = find(father[u]);
    }
    // 判断 u 和 v是否找到同一个根
    bool isSame(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }
    // 将v->u 这条边加入并查集
    void join(int u, int v) {
        u = find(u); // 寻找u的根
        v = find(v); // 寻找v的根
        if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
        father[v] = u;
}
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        init();
        for (int i = 0; i < edges.size(); i++) {
            if (isSame(edges[i][0], edges[i][1])) return edges[i];
            else join(edges[i][0], edges[i][1]);
        }
        return {};
    }
};

可以看出，主函数的代码很少，就判断一下边的两个节点在不在同一个集合就可以了。

其他语言版本

Java

class Solution {
    private int n;  // 节点数量3 到 1000
    private int[] father;
    public Solution() {
        n = 1005;
        father = new int[n];

        // 并查集初始化
        for (int i = 0; i < n; ++i) {
            father[i] = i;
        }
    }

    // 并查集里寻根的过程
    private int find(int u) {
        if(u == father[u]) {
            return u;
        }
        father[u] = find(father[u]);
        return father[u];
    }

    // 将v->u 这条边加入并查集
    private void join(int u, int v) {
        u = find(u);
        v = find(v);
        if (u == v) return ;
        father[v] = u;
    }

    // 判断 u 和 v是否找到同一个根，本题用不上
    private Boolean same(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

    public int[] findRedundantConnection(int[][] edges) {
        for (int i = 0; i < edges.length; i++) {
            if (same(edges[i][0], edges[i][1])) {
                return edges[i];
            } else  {
                join(edges[i][0], edges[i][1]);
            }
        }
        return null;
    }
}

Python

class Solution:

    def __init__(self):
        """
        初始化
        """
        self.n = 1005
        self.father = [i for i in range(self.n)]


    def find(self, u):
        """
        并查集里寻根的过程
        """
        if u == self.father[u]:
            return u
        self.father[u] = self.find(self.father[u])
        return self.father[u]

    def join(self, u, v):
        """
        将v->u 这条边加入并查集
        """
        u = self.find(u)
        v = self.find(v)
        if u == v : return
        self.father[v] = u
        pass


    def same(self, u, v ):
        """
        判断 u 和 v是否找到同一个根，本题用不上
        """
        u = self.find(u)
        v = self.find(v)
        return u == v

    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        for i in range(len(edges)):
            if self.same(edges[i][0], edges[i][1]) :
                return edges[i]
            else :
                self.join(edges[i][0], edges[i][1])
        return []

Python简洁写法：

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        n = len(edges)
        p = [i for i in range(n+1)]
        def find(i):
            if p[i] != i:
                p[i] = find(p[i])
            return p[i]
        for u, v in edges:
            if p[find(u)] == find(v):
                return [u, v]
            p[find(u)] = find(v)

Go

// 全局变量
var (
    n = 1005 // 节点数量3 到 1000
    father = make([]int, 1005)
)

// 并查集初始化
func initialize() {
	for i := 0; i < n; i++ {
		father[i] = i
	}
}

// 并查集里寻根的过程
func find(u int) int {
	if u == father[u] {
		return u
	}
	father[u] = find(father[u])
	return father[u]
}

// 将v->u 这条边加入并查集
func join(u, v int) {
	u = find(u)
	v = find(v)
	if u == v {
		return
	}
	father[v] = u
}

// 判断 u 和 v是否找到同一个根，本题用不上
func same(u, v int) bool {
	u = find(u)
	v = find(v)
	return u == v
}

func findRedundantConnection(edges [][]int) []int {
	initialize()
	for i := 0; i < len(edges); i++ {
		if same(edges[i][0], edges[i][1]) {
			return edges[i]
		} else {
			join(edges[i][0], edges[i][1])
		}
	}
	return []int{}
}

JavaScript

const n = 1005;
const father = new Array(n);
// 并查集里寻根的过程
const find = u => {
    return u == father[u] ? u : father[u] = find(father[u]);
};

// 将v->u 这条边加入并查集
const join = (u, v) => {
    u = find(u);
    v = find(v);
    if(u == v) return;
    father[v] = u;
};

// 判断 u 和 v是否找到同一个根，本题用不上
const same = (u, v) => {
    u = find(u);
    v = find(v);
    return u == v;
};

/**
 * @param {number[][]} edges
 * @return {number[]}
 */
var findRedundantConnection = function(edges) {
    // 并查集初始化
    for(let i = 0; i < n; i++){
        father[i] = i;
    }
    for(let i = 0; i < edges.length; i++){
        if(same(edges[i][0], edges[i][1])) return edges[i];
        else join(edges[i][0], edges[i][1]);
    }
    return null;
};

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

0684.冗余连接.md

0684.冗余连接.md

684.冗余连接

思路

其他语言版本

Java

Python

Python简洁写法：

Go

JavaScript

Files

0684.冗余连接.md

Latest commit

History

0684.冗余连接.md

File metadata and controls

684.冗余连接

思路

其他语言版本

Java

Python

Python简洁写法：

Go

JavaScript