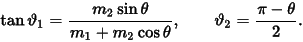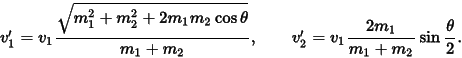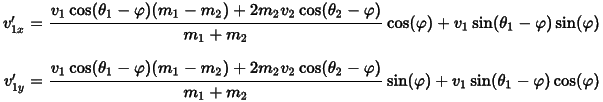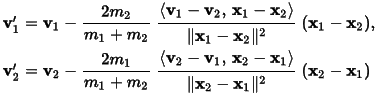For Python language
python simulation.pyWIKIPEDIA
An elastic collision is an encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total kinetic energy before the encounter.
Perfectly elastic collisions occur only if there is no net conversion of kinetic energy into other forms (such as heat or noise) and therefore they do not normally occur in reality.
During the collision of small objects, kinetic energy is first converted to potential
energy associated with a repulsive force between the particles (when the particles
move against this force, i.e. the angle between the force and the relative velocity
is obtuse), then this potential energy is converted back to kinetic energy (when the
particles move with this force, i.e. the angle between the force and the relative
velocity is acute). The collisions of atoms are elastic collisions
(Rutherford backscattering is one example).
Two-dimensional
For the case of two colliding bodies in two dimensions, the overall velocity of each
body must be split into two perpendicular velocities: one tangent to the common
normal surfaces of the colliding bodies at the point of contact, the other along the
line of collision. Since the collision only imparts force along the line of collision,
the velocities that are tangent to the point of collision do not change.
The velocities along the line of collision can then be used in the same equations as a one-dimensional collision. The final velocities can then be calculated from the two new component velocities and will depend on the point of collision. Studies of two-dimensional collisions are conducted for many bodies in the framework of a two-dimensional gas.
In a center of momentum frame at any time the velocities of the two bodies are in
opposite directions, with magnitudes inversely proportional to the masses.
In an elastic collision these magnitudes do not change. The directions may change
depending on the shapes of the bodies and the point of impact.
For example, in the case of spheres the angle depends on the distance between the (parallel) paths of the centers of the two bodies. Any non-zero change of direction is possible: if this distance is zero the velocities are reversed in the collision; if it is close to the sum of the radii of the spheres the two bodies are only slightly deflected.
Assuming that the second particle is at rest before the collision, the angles of deflection of the two particles, v1 and v2, are related to the angle of deflection theta in the system of the center of mass by
The magnitudes of the velocities of the particles after the collision are:
The final x and y velocities components of the first ball can be calculated as
Where v1 and v2 are the scalar sizes of the two original speeds of the objects,
m1 and m2 are their masses, Ɵ1 and Ɵ2 are their movement angles, that is,
v1x = v1cosƟ1, v1y = v1sinƟ1 (meaning moving directly down to the right is either
a -45° angle, or a 315°angle), and lowercase phi (φ) is the contact angle.
(To get the x and y velocities of the second ball, one needs to swap all the '1'
subscripts with '2' subscripts).
This equation is derived from the fact that the interaction between the two bodies
is easily calculated along the contact angle, meaning the velocities of the objects
can be calculated in one dimension by rotating the x & y-axis to be parallel with
the contact angle of the objects, and then rotated back to the original orientation
to get the true x and y components of the velocities In an angle-free representation,
the changed velocities are computed using the centers x1 and x2 at the time of contact
as:
Where the angle brackets indicate the inner product (or dot product) of two vectors.
This library contains the following methods written in Cython and C language:
-
Trigonometry method This equation is derived from the fact that the interaction between the two bodies is easily calculated along the contact angle
-
Angle free method In an angle-free representation, the changed velocities are computed using the centres x1 and x2 at the time of contact as
Those algorithms are intended to work with Python and Pygame, offering a fast solution for solving elastic collision in real time. This library can be used in various projects, 2d Video game, Arcade game, demos such as particles simulation or live objects system that can interact with each others in a 2d cartesian space or game display.
This library is not a particle engine as such, it offers different methods to resolve collision process between objects.
Designed with simplicity, this library can be used to elaborate complex object interactions with a peace of mind.
Angle free method is the fastest algorithm as it does not require trigonometric functions such as (cos, acos, sin, atan2) in order to solve object's vector components. Angle free method rely on vector calculations instead such as (dot product etc) while trigonometry method requires calculation of object's contact angle and angle theta at point of contact prior solving object's resultant vectors v1 & v2.
Considerations:
* The elastic-collision algorithm must be call after the object's collision.
* You have the choice between ec_game & ec_real. These libraries are essentially
identical except for ec_game that offers the possibility to invert the final vectors
trajectories using the flag `invert`. Inverting the flag will provide the correct
solution of the object collision if you were to draw the vectors on a 2d cartesian
system (without the y-axis inverted).
Do not set the flag to True for 2d video game environment (the flag is set to False
by default).
* Trigonometric method is less accurate than the angle free method due to angle
approximation and due to the fact that the library is build on single
precision (float) with an error margin of 1e-5
* Input vectors are not normalized to conserve the total Kinetic energy
If an object position is at the centre of the display, we would have to decrease its (Y) value in order to move it upward and increase its (Y) value to move it downward. In other words, the display's Y-axis is inverted and this has to be taken into account in the elastic collision equations. This can be easily implemented by reversing the (Y) vectors component for each object before or after contact.
- Real domain R(x, y)
| Vector direction | Resultant | Object centre |
|---|---|---|
| v1( 0.707, 0.707) | v1'(-0.707, -0.707) | C1 ( 0, 0) |
| v2(-0.707, -0.707) | v2'( 0.707, 0.707) | C2 (1.414, 1.414) |
figure 1
- Game environement (Y-Axis inverted )
| Vector direction | Resultant | Object centre |
|---|---|---|
| v1( 0.707, 0.707) | v1'(-0.707, -0.707) | C1 ( 0, 0) |
| v2(-0.707, -0.707) | v2'( 0.707, 0.707) | C2 (1.414, 1.414) |
Figure 2
As you can see both domains return the same values.
However, in the real cartesian domain the red ball will be moving at 45 degrees
while and on the game display, the reb ball will be moving at -45 degrees.
In order to convert one model to another, we would have to invert the Y-component of
the solution provided by the elastic-collision equations such as :
| Vector direction | Resultant | y component inverted |
|---|---|---|
| v1( 0.707, 0.707) | v1'(-0.707,-0.707) | v1'(-0.707, 0.707) |
| v2(-0.707,-0.707) | v2'( 0.707, 0.707) | v2'( 0.707,-0.707) |
- The project is under the
MIT license
check the link for newest version https://pypi.org/project/ElasticCollision/
- Available python build 3.6, 3.7, 3.8, 3.9, 3.10 and source build
- Compatible WINDOWS and LINUX for platform x86, x86_64
pip install ElasticCollision
- Checking the installed version (Imported module is case sensitive)
>>>from ElasticCollision.ec_game import __version__
>>>__version__Download the source code and decompress the Tar or zip file
- Linux
tar -xvf ElasticCollision-1.0.3.tar.gz
cd ElasticCollision-1.0.3
python3 setup.py bdist_wheel
cd dist
pip3 install ElasticCollision-xxxxxx - Windows
Decompress the archive and enter ElasticCollision directory
python setup.py bdist_wheel
cd dist
pip install ElasticCollision-xxxxxx# FOR 2D GAME (Y-AXIS INVERTED)
from pygame.math import Vector2
from ElasticCollision.ec_game import momentum_trigonometry
vector1 = Vector2(0.707, 0.707)
centre1 = Vector2(0.0, 0.0)
vector2 = Vector2(-0.707, -0.707)
centre2 = Vector2(1.4142, 1.4142)
mass1 = 1.0
mass2 = 1.0
v11, v12 = momentum_trigonometry(
centre1, centre2, vector1, vector2, mass1, mass2, False)
print(v11, v12)# FOR 2D GAME (Y-AXIS INVERTED)
from pygame.math import Vector2
from ElasticCollision.ec_game import momentum_angle_free
vector1 = Vector2(0.707, 0.707)
centre1 = Vector2(0.0, 0.0)
vector2 = Vector2(-0.707, -0.707)
centre2 = Vector2(1.4142, 1.4142)
mass1 = 1.0
mass2 = 1.0
v11, v12 = momentum_angle_free(
vector1, vector2, mass1, mass2, centre1, centre2, False)
print(v11, v12)== RESTART: C:/Users/yoyob/AppData/Local/Programs/Python/Python36/test11.py ==
pygame 2.0.0 (SDL 2.0.12, python 3.6.3)
Hello from the pygame community. https://www.pygame.org/contribute.html
[-0.707, -0.707] [0.707001, 0.707]
[-0.707, -0.707] [0.707, 0.707]
>>> Each time you are modifying any of the following files
ec_game.pyx, c_game.pyx, ec_real.pyx or any external C code if applicable
1) open a terminal window
2) Go under the directory game
3) run : python setup_ec_game.py build_ext --inplace --force
4) Go under the directory real
5) run : python setup_ec_real.py build_ext --inplace --force
If you have to compile the code with a specific python
version, make sure to reference the right python version
in (python38 setup_ec_real.py build_ext --inplace)
If the compilation fail, refers to the requirement section and
make sure cython and a C-compiler are correctly install on your
system.
- A compiler such visual studio, MSVC, CGYWIN setup correctly on
your system.
- a C compiler for windows (Visual Studio, MinGW etc) install
on your system and linked to your windows environment.
Note that some adjustment might be needed once a compiler is
install on your system, refer to external documentation or
tutorial in order to setup this process.e.g https://devblogs.
microsoft.com/python/unable-to-find-vcvarsall-bat/
Yoann Berenguer
numpy >= 1.18
pygame >=2.0.0
cython >=0.29.21
MIT License
Copyright (c) 2019 Yoann Berenguer
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
>>> from ElasticCollision import *
>>> from ElasticCollision.tests.test_ec_game import run_testsuite
>>> run_testsuite()
>>> from ElasticCollision import *
>>> from ElasticCollision.tests.test_ec_real import run_testsuite
>>> run_testsuite()Links
https://en.wikipedia.org/wiki/Elastic_collision