Matrix Matrix Multiplication in Parallel

How to Use

• git clone https://github.com/zeeshanmahar007/Matrix-Matrix-Multiplication-in-Parallel.git.
• cd Matrix-Matrix-Multiplication-in-Parallel.
• execute code by this command first gcc -fopenmp omp_parallel.c -o omp.out.
• then Run code by this ./omp.out.
• Enter value of Row & Column for Matrix-A then for Matrix-B.

Author

You can get in touch with me on my LinkedIn Profile:

Mahar Zeeshan

You can also follow my GitHub Profile to stay updated about my latest projects:

If you liked the repo then kindly support it by giving it a star ⭐!

Project Documentation

Abstract

In this Report we are developing and implementing Shared memory and distributed memory Algorithm for Parallel matrix-matrix multiplication. The journey start with the description and introduction of the Algorithm we are going to implement. As in this Report we implemented shared memory Algorithm, so we do not need to send or receive any kind of data or must develop special kind of new algorithm. Then we discuss the Rationale and methodology of our Algorithm and then we calculate Cost of Algorithm and compute speedup we achieve by implementing parallel algorithm for Matrix-Matrix Multiplication.

Introduction

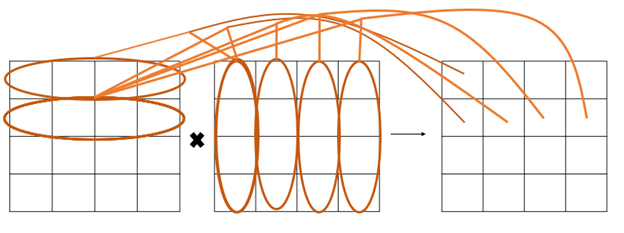
As we know the importance of matrix multiplication and used in many fields like a basic tool of linear algebra, and as such has numerous applications in many areas of mathematics, as well as in applied mathematics, statistics, physics, economics, and engineering. Computing matrix products is a central operation in all computational applications of linear algebra. If we have large matrix then we need large number of times to calculate the product of matrix that is why we are implementing parallel algorithm to save our time. Also, we need high computation power to calculate if we parallel this and dividing into smaller task and then assign them to different processor for parallel execution save our time and computation of idle processor. As now we have multiprocessor machine everywhere that allow us to execute and Run different Application at the same time on different processor if we have this possible then we also do this to divide one task into different subtask and then assign the processor to execute and compute our result at the same time.

Parallelization methodology

In this section we detailed discuss the methodology of our algorithm that how we are going to implement algorithm and how it will work 1st we discuss the shared memory algorithm as we know we use pragmas to parallel loops and other portion of code that need high computation or time. In this Algorithm as we have different loops for computation so we will apply pragmas on loop to parallel them. here we discuss our code. The main multiplication code that we are implemented to calculate the resultant matrix. In 1st line we set dynamic into 0 this means we are giving instruction to create threads according to me and next line we give them 4 to calculate result using these 4 threads. And use collapse clause here that can do is not make all the loops into one loop and then divide into processor.

Here is example of collapse:

If we have this code

Collapse does this:

Here the main code that we parallel is to multiply both matrix

 omp_set_dynamic(0);
 omp_set_num_threads(4);
 //multiply of the matrix;
 #pragma omp parallel for collapse(3) private(i,j,k) shared(row1,col1,mul)
 for(i=0;i<row1;i++)
     {
         for(j=0;j<col2;j++)
            {
                for(k=0;k<row2;k++)
                    {
                        mul[i][j]+=a[i][k]*b[k][j];
                    }
            }
      }

If we see this in MPI then we can implement by seeing this structure

Cost Analysis

This code is executed on different Problem size on 4 threads and run this as a sequential and calculate speedup by dividing Sequential Time with Parallel time.

Speedup = Sequential Time/Parallel Time

Problem Size N	Sequential Time(sec)	Parallel Time(sec) With 4 Threads	Speedup
1000*1000	9.9	8.3	1.19
2000*2000	124.6	22.13	5.63
3000*3000	454.6	21.9	20.75
4000*4000	1134.5	62.06	18.28
5000*5000	23.26	10.8	215.37
6000*6000	3837.05	24.29	157.96
7000*7000	6277.61	69.46	90.37

NOTE: Given Problem Size N is only of one Matrix.

Conclusions

As we seen main code and analysis the code, we conclude that according to our algorithm that we have implemented is if we increase Problem Size then Speedup also increase but at the start speedup is very low due to making like fork the different threads and then join threads also consume time that is why we have low speedup at the start or if we give low problem size.